Luminance Meters and Colorimeters
Luminance Meter
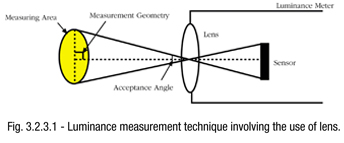
The visible energy output of a light source can be determined with a luminance measurement. Luminance is a directional quantity and, hence, we have to specify the acceptance angle of the instrument, measured area, and measurement geometry with respect to the source, in order to communicate the luminance measurements effectively. These factors are important as most light sources are not perfect lambertian sources (luminance is the same in all direction) and might not be uniform in luminance throughout the sources.
Since measurement is targeted at the source, such measurement can be achieved by using a optical lens system. Both the angular field of view and the angle subtended by the objective lens should be limited to avoid collecting light from parts of the display at slightly different angles.
Luminance measurement are important for products, such as traffic lights, televisions, and tail lights of automobiles.
Illuminance Meter
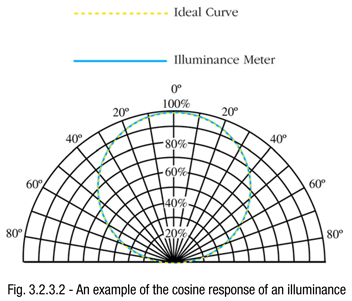
Illuminance is a measure of visible energy falling upon an object’s surface. Illuminance measurements are particularly susceptible to errors caused by off-axis light. By definition, light at the measurement plane should be proportional to the cosine of the angle at which the light is incident. However, due to total integration of the sensor into the detector head or the illuminance meter itself, many illuminance meters do not naturally collect light correctly according to the cosine law.
Cosine correction feature is included in the illuminance meter by means of a cosine diffuser which is placed over the sensor and filter. It is important to note that different systems will generate different cosine responses which result indifferent cosine errors at different incident angles due to the nature of the system geometry. Therefore, it is important to understand the system cosine response when comparing illuminance measurements from different illuminance meters, especially when off-axis light measurement is concerned.
Luminous Flux Meter
Luminous flux measurement is to determine the total visible energy emitted by a light source. An integrating sphere is often used to converge all the power emitted by the source to the detector head.
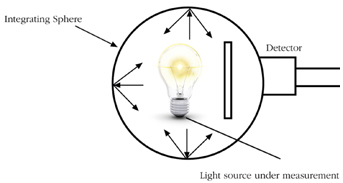
The integrating sphere has to be large enough to encompass the light source being measured, and as a general rule,the larger the sphere, the smaller the errors in measuring luminous flux for different light sources. As a rough example,calibrating a 1.5m tubular lamp in a 2.5m diameter sphere against a small incandescent standard will produce half the error that would result from calibration the same lamp in a 2m sphere. Calibration of such integrating sphere can be carried out by means of transfer lamp standards which are traceable to recognized national standards. A good quality integrating sphere which postulates the performance of an ideally spherical, evenly coated interior requires a huge investment and usually have to be customized to the light measurement application. Hence, the existence of a general purpose luminous flux meter is very limited.
Luminous Intensity Meter
Luminous intensity represents the flux flowing out of a source in a given direction per solid angle and it is used to quantify the power of a light source. As the definition implies, luminous intensity measurement involves several geometrical intricacies, such as measurement direction and amount of solid angle. Light sources are rarely spatially homogeneous, leading to the questions on which direction and how much solid angle should be used to carry out the measurement.
Hence, to measure the luminous intensity of a light source meaningfully, an agreed-upon fixture that defines the solid angle encompassed by the measurement and that orients the light source repeatedly in an specified direction must be used. In other words, such meters have to be configured for the geometry of the source under test. Basically, there are no off-the-shelf luminous intensity meters and comparison of measured data from two different luminous intensity meters serve no purpose, unless their measurement geometries are identical.

Note: Solid angle can be calculated from the known detector’s area and measurement distance. Detector is used to measure the flux reading in lumen.
Three Filter Colorimeter
Instruments designed for measuring colored light, which make use of three filters whose spectral sensitivity are matched to the CIE tristimulus color matching functions, are known as three-filter colorimeters. Besides chromaticity measurement, these meters usually include one of the four basic photometric measurements, i.e., luminance, illuminance, luminous intensity, or luminous flux measurement.
These instruments use detectors which comprise high quality photodiodes with series-connected filters. The incident light is converted by the detector into signals which directly yield the standard XYZ tristimulus values.
Nevertheless, matching to the standard CIE tristimulus curves can be achieved only with finite accuracy. Deviations will occur in the defined CIE curves and in the sensitivity curves of the measuring instrument. These differences are negligible as long as the light to be measured exhibits a continuous energy output over the entire visible spectrum. However, the error may be significant if steep edges or spectral lines occur in the spectrum. Hence, three-filter colorimeters are not usually suited to measure light sources with spectral lines, e.g., discharge lamps (refer to Fig.3.2.3.5a), or with narrow spectral energy distributions, e.g., LEDS (refer to Fig.3.2.3.5b).
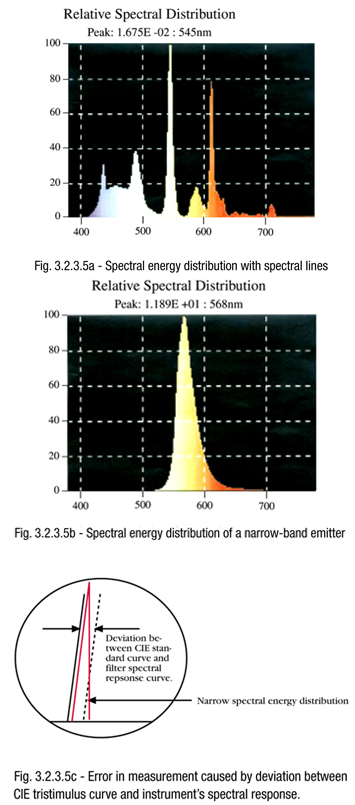
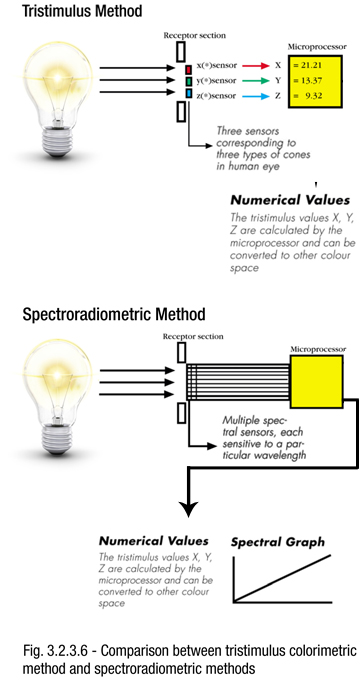
Spectroradiometer
Spectroradiometers are most ideal for measuring spectral energy distribution of the light source, which determine not only the radiometric and photometric quantities, but also the colorimetric quantities of light. These instruments record the radiation spectrum of the light source and calculate the desired parameters, such as chromaticity and luminance. Dispersion of light is usually accomplished in spectroradiometer by means of prisms or diffraction gratings.
The exact CIE V* curve and CIE color matching curves are stored in the software and are used to process the data from the measured spectral energy distribution of the light source under test. Hence, the measurement error associated with photometers and filter colorimeters is avoided in spectroradiometers. However, adequate sensitivity, high linearity, low stray light, low polarization error, and a spectral bandpass resolution of 5 nm or less are essential for obtaining good accuracy.
Non-thermal radiators, such as discharge lamps (which can be characterized by their non-continuous spectral energy distribution), and narrow-band emitters can only be measured with precision by means of the spectral procedure.
When compared to three-filter colorimeters, spectroradiometers do have their limitations, in terms of speed of measurement, price and portability.